Условия, ветвление, отладка. Циклы.

Представление целых чисел в памяти компьютера

Есть различные способы хранить знаковые целые числа в памяти. Один из них — sign-magnitude, то есть первый бит отведен на знак, остальные — на модуль. Это кажется более естественным, но только не для компьютера.

Например: \(-6\) в sign-magnitude будет представлено как 1110, где 1 — знак (отрицательный), а 110 — модуль (\(110_2 = 4 + 2 = 6_10\))

Бинарное значение Sign-magnitude Беззнаковое
\(00000000\) \(0\) \(0\)
\(00000001\) \(1\) \(1\)
\(\ldots\) \(\ldots\) \(\ldots\)
\(01111111\) \(127\) \(127\)
\(10000000\) \(-0\) \(128\)
\(10000001\) \(-1\) \(129\)
\(\ldots\) \(\ldots\) \(\ldots\)
\(11111111\) \(-127\) \(255\)

В sign-magnitude первый бит — знак, остальные — модуль. В беззнаковом представлении все биты — значение.

В качестве примечания стоит отметить способ, как можно легко представлять в двоичной системе степени двойки: \[2^0 = 1 = 1_2\] \[2^1 = 2 = 10_2\] \[2^2 = 4 = 100_2\] \[ 2^n = 1 \underbrace{0 \dots 0}_{n} \] \[ 2^n - 1 = 1 \underbrace{0 \dots 0}_{n} - 1 = \underbrace{1 \dots 1}_{n} \] Запомнив примеры выше, возможно моментально переводить такие числа как \(255\), \(1023\), \(2048\), \(8\) и их двоичные представления.

Возвращаемся к способам хранения целых чисел. Итак, двоично-дополнительный код — это способ представления отрицательных целых чисел в памяти компьютера. Он позволяет выполнять арифметические операции над знаковыми числами так же просто, как и над беззнаковыми.

Как получить двоично-дополнительное представление отрицательного числа:

  1. Записать абсолютное значение числа в двоичной системе, используя необходимое количество бит.
  2. Инвертировать все биты (заменить 0 на 1, а 1 на 0).
  3. Прибавить 1 к полученному числу.

Пример:
Получим представление числа \(-6\) в 4-битном двоично-дополнительном коде.

  • \(+6\) в двоичном виде: 0110
  • Инвертируем все биты: 1001
  • Прибавляем 1: 1001 + 1 = 1010

Таким образом, \(-6\) в 4-битном двоично-дополнительном коде — это 1010.

Проверка:

Бит \(1\) \(0\) \(1\) \(0\)
Значение \(-8\) \(4\) \(2\) \(1\)

\(1010 = -8 + 0 + 2 + 0 = -6\)

То есть первый бит отвечает за \(-2^{n-1}\), а остальные биты — за положительные степени двойки.

Таблица 4-битных двоично-дополнительных чисел

Биты Десятичное значение
\(0000\) \(0\)
\(0001\) \(1\)
\(0010\) \(2\)
\(\ldots\) \(\ldots\)
\(0111\) \(7\)
\(1000\) \(-8\)
\(1001\) \(-7\)
\(\ldots\) \(\ldots\)
\(1110\) \(-2\)
\(1111\) \(-1\)

Замечание:
Инвертирование и прибавление 1 — это универсальный способ получить противоположное число в двоично-дополнительном коде. Например, чтобы получить \(-n\), достаточно инвертировать все биты числа \(n\) и прибавить 1.

Двоично-дополнительный код имеет несколько преимуществ: - не требуется отдельная логика для определения знака числа; - арифметические операции (сложение, вычитание) выполняются одинаково

Рассмотрим последний пункт чуть подробнее: что будет. если многократно прибавлять 1 к некоторому знаковому 8-битному числу, начиная с \(-128\), то есть наименьшего возможного значения?

Биты Десятичное значение Комментарий
\(10000000\) \(-128\)
\(10000001\) \(-127\)
\(\ldots\) \(\ldots\)
\(11111111\) \(-1\) \(11111111_2 + 1_2 = 100000000_2\). Записываем 8 правых бит
\(00000000\) \(0\)
\(00000001\) \(1\)
\(\ldots\) \(\ldots\)
\(01111111\) \(127\)
\(10000000\) \(-128\) “Зацикливание”, то есть произошло “переполнение”, “overflow”
\(\ldots\) \(\ldots\)

Переполнение целых типов

Что же произойдет, если попытаться сохранить слишком большое значение в переменную маленького размера? Например, число \(300\) в тип unsigned char (целое, беззнаковое, 8 бит).

\(300_{10} = 100101100_2\), занимает больше, чем \(9\) бит. Запишем правые \(8\) бит в нашу переменную, тогда в ней окажется \(00101100_2 = 101100_2 = 32 + 8 + 4 = 44_{10}\). Таким образом, явно ошибка выведена не будет, программа продолжит исполнение. Можно заметить, что переполнение типа соответствует взятию остатка при делении на \(2^{\operatorname{sizeof}(T)}\) в данном случае \(2^{8 \operatorname{bit}} = 256\).

Если программа будет прибавлять по 1 к некоторой переменной целого типа, то после 254 у типа char последует 255, 0, 1, 2 и так далее, так как это число беззнаковое и \(255 = 2^8 - 1\).

Покажем эту идею на примере:

#include <iostream>

int main() {
    unsigned char c_1 = 0;
    c_1 -= 1; // происходит underflow
    std::cout << (int)c_1 << '\n'; // 255

    c_1 = 300;
    std::cout << (int)c_1 << '\n'; // 44
}

Если не использовать (int)c_1  при выводе char, то число будет воспринято как код символа и будет выведена запятая или буква латинского алфавита. Этот способ явного приведения типов пришел к C++ из языка С. Рекомендуется использовать static_cast<int>(c_1) вместо (int)c_1, так как это более явно и безопасно. В примере был использован именно C-style кастинг для краткости

Условия

Логические операции

Операции сравнения соответствуют алгебре логики, которая рассматривалась на уроках информатики:

  • отрицание – НЕ, которое инвертирует (заменяет на противоположное) логическую переменную. \(\lnot A\), !A

  • конъюнкция – И, логическое умножение, истинно только при истинности обеих входящих переменных: \(A \land B\), A && B

  • дизъюнкция – ИЛИ, логическое сложение, истинно, если истинна любая из входящих переменных: \(A \lor B\), A || B

\(A\) \(\lnot A\)
0 1
1 0
\(A\) \(B\) \(A \land B\)
0 0 0
0 1 0
1 0 0
1 1 1
\(A\) \(B\) \(A \lor B\)
0 0 0
0 1 1
1 0 1
1 1 1

Такие логические операции предстоит использовать, если мы захотим потребовать, чтобы некоторые условия должны соблюдаться одновременно (конъюнкция), “хотя бы какое-то условие” (дизъюнкция). Например, положительность числа можно записать следующим образом:

\[ \begin{gathered} A = \Big\{ \text{число является отрицательным} \Big\} = \Big\{ x < 0 \Big\} \\ B = \Big\{ \text{число не равно } 0 \Big\} = \Big\{ x \ne 0 \Big\} \\ C = \Big\{ \text{число является положительным} \Big\} = \Big\{ x > 0 \Big\} \\ \text{ }\\ \ С \equiv \lnot A \land B \\\text{ }\\ \Big\{ x > 0 \Big\} \equiv \Big\{ x \ge 0 \Big\} \land \Big\{ x \ne 0 \Big\} \end{gathered} \]

Операторы сравнения

Оператор сравнения — некоторый логический оператор, который возвращает тип bool – логическое значение

  • > (больше)

  • >= (больше или равно)

  • < (меньше)

  • <= (меньше или равно)

  • == (равно)

  • != (не равно)

Синтаксис

if (<cond>) {
    // Если условие выполняется, то программа зайдет в эту область кода
} else {
    // Иначе: то есть если условие НЕ выполняется, то программа зайдет в эту область кода
}
// исполнение программы продолжится здесь вне зависимости от условия
#include <iostream>
#include <cmath>

int main() {
    int age;
    std::cin >> age;
    if (age > 12) {
        printf("You are %d years old, so, you're too old for this cartoon\n", age);
    } else {
        printf("You are %d years old, so, you're young enough for this cartoon. Enjoy!\n", age);
    }
}

Отлично! Теперь мы умеем писать простейшие условия с введенными переменные. Если же у нас есть множество вариантов развития событий, то мы можем все их предусмотреть расширенным синтаксисом условий:

if (condition1) {
    // случай, когда condition1 истинно
} else if (condition2) {
    // случай, когда condition1 ложно, а condition2 истинно
} else if (condition3) {
    // случай, когда condition1 и condition2 ложны, а condition3 истинно
} else {
    // случай, когда condition1, condition2 и condition3 ложны
}

Это дает нам неограниченные возможности изменения логики линейной программы. Например, давайте напишем контролер билетов в кино. Пусть все настоящие билеты умеют номер, который не делится на 6 и оканчивается на четную цифру. Также нужно предусмотреть пропуск сотрудников, у которых номера билетов меньше 10, и директора кинотеатра, который обладает билетом с номером 777.

#include <iostream>

int main() {
    int age;
    std::cin >> age;
    if (age > 12) {
        printf("You are %d years old, so, you're too old for this cartoon\n", age);
    } else {
        printf("You are %d years old, so, you're young enough for this cartoon. Enter the number of your\n", age);

        int ticket_id;
        printf("Enter your ticket ID:\n", age);
        std::cin >> ticket_id;
        if (ticket_id % 6 != 0 && (ticket_id % 10) % 2 == 0) {
            printf("Enjoy the movie, customer!\n");
        } else if (ticket_id >= 0 && ticket_id < 10) {
            printf("Hi! Have a nice day at work, employee\n");
        } else if (ticket_id == 777) {
            printf("Glad to see you again, the CEO!\n");
        } else { // неверный номер билета, так как ни одно из условий не было выполнено
            printf("Invalid ticket ID! Call staff for support\n");
        }

    }
    printf("Program finished\n");

}

Как показано на примере выше, к целым числам можно применять любой оператор сравнение, но с числами с плавающей точкой все обстоит немного сложнее. Вследствие особенностей их хранения, которые были рассмотрены выше, допустимо малая неточность в интерпретации записи чисел: записанное как 3.0 может быть прочитано как 3.0000001 или 2.99999999 – такое небольшое отклонение называют пределом точности при хранении числа с плавающей точкой. При сложных и масштабных вычислениях такая ошибка может накапливаться и существенно влиять на результат, поэтому в сложных математических программах учитывают некоторую погрешность результата при вычислениях, применяют алгоритмы для уменьшения этого отклонения.

Рассмотрим корректный вариант проверки равенства переменно float некоторому значению:

#include <iostream>
#include <algorithm>

int main() {
    float number;
    std::cin >> number;

    // if (number == 3.0) {
        // INCORRECT
    // }

    if (std::abs(number - 3.0) < 0.000001) { // проверяем на равенство числу 3.0
        std::cout << "you have entered 3.0\n";
    }

    printf("Program finished\n");

}

Операторы && и || в составных условиях не будут проверять лишние условия, если таковые появятся в вашей программе. Например, как только оператор || увидит, что первый операнд истинен (true), то второй операнд проверяться не будет. Аналогично и с конъюнкцией – логическим И (&&): если первый операнд false, то второй операнд проверяться не будет, ведь итог уже ясен (см. таблицы истинности выше).

Switch-case

Если нам предстоит проверить переменную на равенству множества значений, то имеет смысл использовать особую конструкцию языка – switch. Она принимает некоторую переменную переменную на вход, а затем пытается последовательно пройтись по условию и найти точное совпадение с указанными значениями.

#include <cstdint>
#include <iostream>

int main() {
    int64_t a, b;
    char operation;
    std::cin >> a >> operation >> b;

    int64_t result = 0;
    if (operation == '+') {
        result = a + b;
    } else if (operation == '-') {
        result = a - b;
    } else if (operation == '*') {
        result = a * b;
    } else if (operation == '/' || operation == ':') {
        result = a / b;
    } else if (operation == '%') {  // остаток от деления
        result = a % b;
    }

    std::cout << result << "\n";
}

Такой не самый красивый перебор точных равенств можно заменить следующей конструкцией:

#include <cstdint>
#include <iostream>

int main() {
    int64_t a, b;
    char operation;
    std::cin >> a >> operation >> b;

    int64_t result;
    switch (operation) {
        case '+':
            result = a + b;
            break;  // если не написать этот break, программа просто пойдёт дальше в код следующего блока case
        case '-':
            result = a - b;
            break;
        case '*':
            result = a * b;
            break;
        case '/':
        case ':':
            result = a / b;
            break;
        case '%':
            result = a % b;
            break;
        default:  // здесь обрабатывается случай, когда ни один case не сработал.
            result = 0;
    }

    std::cout << result << "\n";
}

Важно помнить, что переменная, которая рассматривается в switch должна быть элементарным типом (как правило, числом), std::string уже не подойдет.

Задача о принадлежности точки некоторой области

Вспомним с уроков математики, что если у нас есть график некоторой функции \(f(x)\), то область над графиком будет множеством точек, которые удовлетворяют условию \(y \ge f(x)\). Область под графиком – \(y \le f(x)\). Строгость неравенства будет отвечать за включение самой границы (графика нашей изначальной функции) в область.

Тогда любую область мы можем задать как объединение и пересечение некоторых областей. Рассмотрим вот такую задачу:

Задача 112166 на использование условий

Как мы можем описать закрашенную область:

  • ниже \(y = \sin x\)

  • ниже \(y = 0.5\)

  • выше \(y = 0\)

Напишем код для решения такой задачи:

#include <iostream>
#include <cmath>

int main() {
    float x, y;
    std::cin >> x >> y;
    if (y <= std::sin(x) && y >= 0 && y <= 0.5) {
        printf("YES\n");
    } else {
        printf("NO\n");
    }

}

Решение задачи 112166 на использование условий

Отладка программ

После написание программы вы непременно столкнетесь с набором проблем: ошибкой компиляции, отсутствием вывода, некрасивый вывод ответа в консоль и еще миллион мелочей. Такие ошибки можно без труда исправить: прочитать сообщения и предложения компилятора, поправить вывод; а вот ошибку во время выполнения программы (run time error) или ошибку в логике уже не так и легко обнаружить и исправить. Рассмотрим практические способы поиска ошибок в коде.

Разбор случаев вне программы

Зная реализованную логику, возможно придумать входные данные программе, а затем вручную проследить за поведением программы “на бумаге”. Вы понимаете, какие промежуточные значения ожидаете от программы, и при несовпадении ожиданий и значений на бумаге, вы понимаете, какую операцию или логику реализовали неверно, и можете ее исправить в коде.

Основной минус такого подхода – сложность прогона больших разветвленных программ на бумаге.

Трассировка

Идея заключается в написании дополнительного вывода в программе: так вы можете проследить, куда программа приходит при ветвлении, какие промежуточные значения имеет. Если внимательно читать вывод (или, как еще его называют – логи), то можно многое понять о программе. Это полноправный способ, который позволяет быстро получить понимание, что идет не так. Основной минус: программа продолжает выполнение с прежней скоростью, понимание ее логике вы пытаетесь восстановить по полученному выводу, что не всегда удобно или даже возможно.

Отладчик

Если специальные программы (наподобие компилятора), которые по скомпилированному исполняемому файлу с записанной дополнительной информацией могут показать вам все промежуточные переменных, остановить программу на любой строке, позволить вам пройтись вместе с вашей программой строка за строкой и проследить, что и на каком этапе идет не так.

Рассмотрим отладчик подробнее:

  • breakpoint (“точка останова”) – ваша пометка строки, на которой отладчику нужно остановиться и спросить вас о дальнейших действиях. Вы можете ставить неограниченное количество таких отметок

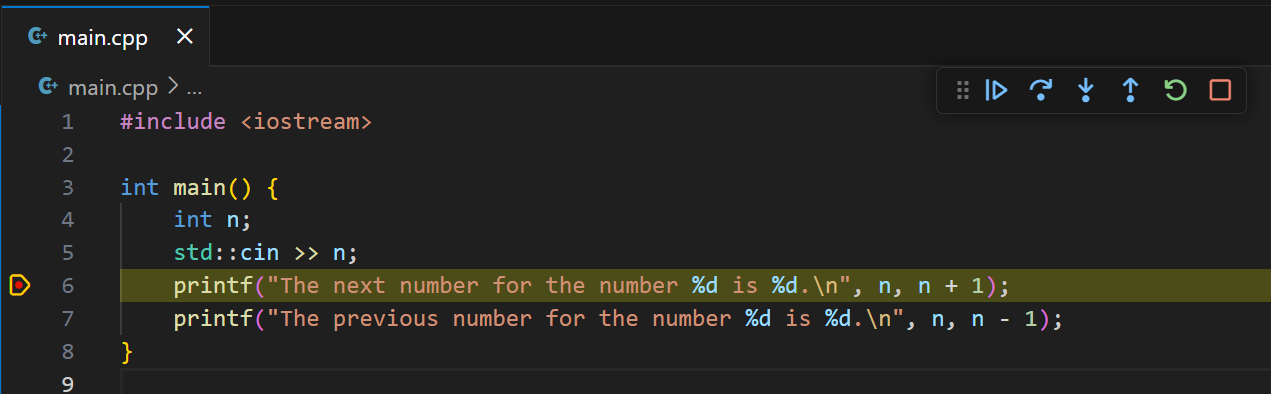Breakpoint и выделение строки при остановке Breakpoint и выделение строки при остановке

  • окно переменных – здесь можно посмотреть значения переменных на данный момент, сверить их с вашими ожиданиями в контексте задачи

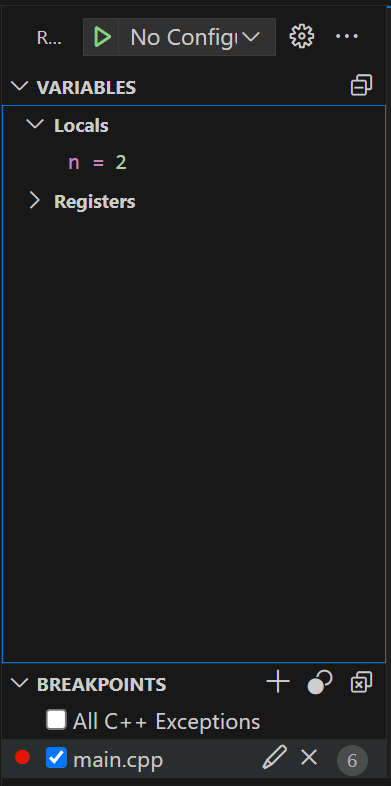    Окно с переменными Окно с переменными

  • набор команд отладчика (далее слева направо)

    • Continue – программа выйдет из режима ожидания, начнет выполнение в обыкновенном режиме до следующей точки останова (breakpoint)

    • Step over – программа перейдет на следующую строку, которая должна быть выполнена, и остановится на ней

    • Step into – если в текущей строке есть вызовы функций или неявные преобразования, то программа “провалится” в внутренние функции (будет актуально во начале второго модуля курса)

    • Step out – противоположно Step into – программа выполнит все строки до прыжка во внешнюю функцию/модуль. Поднявшись на уровень наверх, программа снова остановится

    • Restart – немедленное завершение программы, запуск сначала

    • Stop – немедленное завершение программы, выход из отладчика

Идущий далее материал не является обязательным к прочтению и не будет включен в элементы контроля

Представление чисел с плавающей точкой

Рассмотрим формат хранения чисел с плавающей точкой на примере 32-битного типа float. Для наглядность можно пользоваться калькулятором.

\(\underbrace{1 \text{ bit}}_{\text{sign}} \underbrace{8 \text{ bit}}_{\text{exp}} \underbrace{23 \text{ bit}}_{\text{mantissa}}\)

  1. sign Знаковый бит. Один, старший бит. 0 – число положительное, 1 – отрицательное.

  2. exp Показатель степени. 8-битное целое число, занимает биты с 23-го по 30-ый. Означает степень двойки, на которую будет домножаться основаная часть числа (мантисса)

  3. mantissa Дробная часть (мантисса). 23-битное целое число, содержащее значащие биты вещественного числа.

Интерпретация числа зависит от значения экспоненты:

  • Если \(0 \le exp \le 254\), то число называется нормализованным и равняется \((−1)^{sign} \times 2^{exp−127} \times \text{1.[mantissa]}\). Стоит обратить внимание на вычитание 127 из показателя, так мы получаем возможность записывать как положительные, так и отрицатльные показатели

  • Если \(exp = 0\), то число называется денормализованным и равняется \((−1)^{sign} \times 2^{−126} \times \text{0.[mantissa]}\)

  • Если \(exp = 255, mantissa =0\), то число равно \(\pm \text{inf}\)

  • Если \(exp = 255, mantissa \ne 0\), то число равно \(nan\) или \(NaN\) – not a number – “нечисло” используется для обозначения неверных операций, например, деления на 0 или извлечения арифметического корня из отрицательного числа

Интересный факт:

Вещественные числа становятся более разреженными при увеличении их модуля. Чем число ближе к нулю, тем оно ближе к ближайшему к нему другому представимому числу. А точнее, денормализованные числа идут через одинаковый шаг. Нормализованные числа с \(exp = 1\) идут через удвоенный шаг, с \(exp = 2\) – через учетверённый, и так далее. Иллюстрация распределения чисел:

Распределение чисел с плавающей точкой

Наименьшее нормализованное число: \(2^{-126} \cdot 1.0\). Наибольшего денормализованное число: \(2^{-126} \cdot 0.111111...\) Таким образом, наименьшее нормализованное больше наибольшего денормализованного числа.

Тип double хранится аналогично, но занимает 64 бита: 1 на знак, 11 на экспоненту, 52 на мантиссу.

Вопросы в качестве упражнения (приходите обсуждать ответы до/после пары, если будет время и желание): - почему нельзя точно записать любое рациональное число в памяти компьютера? - как точность записи рационального числа зависит от его модуля? при чем здесь экспонента (exp) при записи в память? - сколько есть способов записать 0? - как перемножить 2 float? то есть как манипулировать какими частями битовой записи, чтобы это было эффективно?

Целочисленные типы

На первой лекции мы рассмотрели знаковые и беззнаковые целые типы, а также модификаторы размера (long и short). На практике проще и понятнее явно указывать, какой тип вы хотите использовать. В этом помогут типы из заголовочного файла <cstdint>:

#include <cstdint>

int8_t a;      // 8-битный знаковый целый
uint8_t b;     // 8-битный беззнаковый целый
int16_t c;     // 16-битный знаковый целый
uint16_t d;    // 16-битный беззнаковый целый
int32_t e;     // 32-битный знаковый целый
uint32_t f;    // 32-битный беззнаковый целый
int64_t g;     // 64-битный знаковый целый
uint64_t h;    // 64-битный беззнаковый целый

Циклы

На прошлой паре были рассмотрены первые конструкции, которые позволяли выполнять программу нелинейно – применять ветвление. Теперь нужно научиться повторять блоки кода несколько раз. В этом нам помогут циклы.

Цикл в программировании – многократное повторение некоторых команд. Он может включать другие циклы, условия, инструкции.

Цикл состоит из:

  • тела цикла – того блока кода, который будет повторяться

  • условия продолжения выполнения цикла

  • итерацией будем называть однократное исполнение тела цикла.

Цикл for

Этот цикл мы, как правило, используем, когда знаем, какое количество итераций нужно будет совершить. Чуть позже будет показано, почему использована оговорка “как правило”.

Пример использования цикла for для вывода последовательных натуральных чисел от \(1\) до \(n\) не включительно.

#include <iostream>

int main() {
    int n;
    std::cin >> n;

    for (int i = 1; i < n; ++i) {
        printf("%d\n", i);
    }
}

Стоит обратить внимание на следующие вещи:

  • после ключевого слова for в круглых скобках можно перечислить через точку с запятой:

    • объявление локальных переменных цикла или изменить их значение перед первой итерацией

    • условие продолжения цикла. Пока оно истинно, цикл будет уходить на следующую итерацию

    • изменение переменных после каждой итерации. Эта инструкция, как правило, необходима: мы ведь хотим как-то влиять на условие, чтобы оно в какой-то момент изменилось

  • переменная i является локальной, ее использование возможно только внутри тела цикла

  • вместо i < n возможно написать любое условие, например, сделать так чтобы выводились последовательные натуральные числа от \(1\) до \(n\) включительно: i <= n

Следующий пример призван продемонстрировать, что описанные выше части цикла for могут быть разными:

#include <iostream>

int main() {
    int n;
    std::cin >> n;

    for (int i = n; i >= 0; i -= 1) {
        printf("%d\n", i);
    }
}

Рассмотрим задачу о нахождении следующей суммы:

\(1 + (1 + 2) + (1 + 2 + 3) + \dots + (1 + 2 + \dots + n)\)

#include <iostream>
// #include <cstdint>

int main() {
    unsigned long long int n; // uint64_t n;
    std::cin >> n;
    unsigned long long int sum = 0;
    unsigned long long int last_add = 1;

    for (unsigned long long int i = 2; i < n + 2; ++i) {
        sum += last_add;
        last_add += i;
    }
    std::cout << sum << '\n';
}

Чуть позже на курсе мы будем активно использовать циклы for для обработки массивов – наборов переменных известного типа. Такой выбор цикла можно объяснить тем, что во время его начала мы знаем размер массива, значит, там известно необходимое количество итераций.

Range-based for

Как можно было заметить, классический цикл for в C++ не является прямым аналогом цикла for из Python. Это исправляет возможность написать цикл так, чтобы он буквально итерировался по объекту. Например, по строке:

#include <iostream>
#include <string>

int main() {
    std::string name;
    printf("Enter your name:\n");
    std::getline(std::cin, name);

    printf("Let me spell it:\n");
    for (char letter: name) {
        std::cout << letter << '\t' << static_cast<int>(letter) << '\n';
    }
    std::cout << '\n';
}

Вывод этой программы:

Enter your name:
Nikolai
Let me spell it:
N   78
i   105
k   107
o   111
l   108
a   97
i   105

“Под капотом” это работает следующим образом:

  • берется “начало” объекта, по которому можно итерироваться (проходиться циклом)

  • пока мы не дошли до “конца” объекта, запускаем итерацию на текущем элементе и переходим к следующему. Мы можем перейти к следующему, благодаря свойству итерируемости

  • когда дошли до “конца” объекта, выходим из цикла

Мы подробно познакомимся и научимся работать с “началом” и “концом” объекта на предстоящих темах курса. Ими окажутся итераторы

Цикл while (с предусловием)

Этот цикл применяется, когда там неизвестно количество итераций, которое нужно будет совершить. Также его можно понимать как синтаксически облегченный цикл for, ведь все, что он предоставляет – это условие продолжения цикла и тело цикла.

Для примера вспомним, как получать цифры известного числа в некоторой системе счисления. Для получения \(i\)-той цифры с конца, нужно найти значение следующего выражения (нумерация с нуля):

\(\text{digit}_i = N / d^{\ i} \ \% \ d\)

Реализуем это в программе, заметим, что 0 при целочисленном делении получится только когда у нас оставалась последняя цифра. Действительно:

\(a / b = 0 (a, b > 0) \Leftrightarrow a < b\)

Сама программа, которая выводит на экран все цифры числа:

В каком порядке она это сделает? Как нужно модифицировать программу, чтобы она выводила цифры в системе счисления \(d\)? Как в таком случае поступить с остатками, которые больше \(9\)?

#include <iostream>

int main() {
    int num;
    std::cin >> num;
    while (num) {
        std::cout << num % 10 << '\n';
        num /= 10;
    }
}

Цикл do-while (с постусловием)

Если при написании программы мы уверены, что цикл должен выполниться хотя бы один раз, то мы можем использовать конструкцию do-while.

Этот цикл используется редко, в нем можно запутаться, если использовать неаккуратно.

#include <iostream>

int main() {
    int n = 1;
    do {
        std::cout << n << "\t" << n * n << "\n";
        ++n;
    } while (n <= 10);
}

Операторы break и continue

  • break – прерывает исполнение итерации и выходит из цикла. Перемещает исполнение программы сразу после тела цикла

  • continue – прерывание исполнение итерации и переходит к следущей, если условие цикла по-прежнему выполняется. В случае цикла for инструкция после итерации будет выполнена ( ++i, например)

Например, сделаем наш калькулятор бесконечным, а выходить из цикла будем, если нам везде ввели нули:

#include <cstdint>
#include <iostream>

int main() {
    int64_t a, b;
    char operation;
    while (true) {
        std::cin >> a >> operation >> b;
        if (!a && !b && operation == '0') {
            break;
        }

        int64_t result = 0; // почему здесь не будет двойного объявления переменной?
        if (operation == '+') {
            result = a + b;
        } else if (operation == '-') {
            result = a - b;
        } else if (operation == '*') {
            result = a * b;
        } else if (operation == '/' || operation == ':') {
            if (!b) {
                continue;
            }
            result = a / b;
        } else if (operation == '%') {  // && b
            if (b) {
                result = a % b;
            }
        }

        std::cout << result << "\n";
    }
}

Условия можно писать множеством разных способов.

Здесь стоит обратить внимание на early exit (“ранний выход”) – когда в функции или цикле не делает множество проверок, которые увеличивают уровни вложенности, а вызывается прерывание итерации.

Например,

// early exit
if (!b) {
    continue;
}
// some very long and important code 1
// some very long and important code 2
// some very long and important code 3

// ====================================

// более стандартный поход
if (b) {
    // some very long and important code 1
    // some very long and important code 2
    // some very long and important code 3
}

Считается, что второй вариант менее читаем из-за того что нужно долгое время помнить о условии, блок кода которого мы сейчас рассматриваем. Но вообще codestyle (правила оформления кода) такого рода является очень относительным понятием :)

Вложенные циклы

Пример вывода таблицы умножения. Для этого мы используем вложенные циклы: для каждого значения переменной i мы печатаем целую строку с помощью цикла по переменной j.

#include <iostream>

int main() {
    for (int i = 1; i <= 10; ++i) {
        for (int j = 1; j <= 10; ++j) {
            std::cout << i * j << "\t";
        }
        std::cout << "\n";
    }
}
1   2   3   4   5   6   7   8   9   10
2   4   6   8   10  12  14  16  18  20
3   6   9   12  15  18  21  24  27  30
4   8   12  16  20  24  28  32  36  40
5   10  15  20  25  30  35  40  45  50
6   12  18  24  30  36  42  48  54  60
7   14  21  28  35  42  49  56  63  70
8   16  24  32  40  48  56  64  72  80
9   18  27  36  45  54  63  72  81  90
10  20  30  40  50  60  70  80  90  100

Использование инструкций break и continueизменит поведение только того цикла, в котором они были вызваны, и не повлияет на внешний цикл.

Типовые приемы в задачах на циклы

Счетчик

Хотим узнать, какое количество объектов удовлетворяет некоторому условию, для этого:

  • создаем переменную, которую будем инкрементировать – счетчик

  • итерируемся по объектам – целым числам из отрезка, элементам последовательности

  • если верно некоторое условие, то увеличиваем счетчик на 1

  • счетчик можно сбрасывать при некотором условии, если нас интересует непрерывное соблюдение условия

В конце такого обхода счетчик будет равен количество объектов, для которого верно условие.

Пример:

#include <iostream>

int main() {
    int new_num;
    std::cin >> new_num;

    int cnt = 0;
    while (new_num) {
        if (new_num % 2 == 0) {
           ++cnt;
        }
        std::cin >> new_num;
    }

    std::cout << cnt << std::endl;

    return 0;
}

Менее естественный (“в дикой природе” не встретится) пример той же самой логики с циклом for:

#include <iostream>

int main() {
    int new_num;
    std::cin >> new_num;

    int cnt;
    for (cnt = 0; new_num != 0; std::cin >> new_num) {
        cnt += (new_num + 1) % 2;
    }

    std::cout << cnt << std::endl;

    return 0;
}

Поиск максимума/минимума

Хотим по итогам прохода по отрезку или последовательности, иметь представление о наибольшем или наименьшем значении, которое встретилось, для этого:

  • создаем переменную, которая равна первому элементу (либо заведомо меньшему или большему значению, чем любой элемент)

  • для каждого элемента обновляем минимум или максимум

#include <iostream>
#include <algorithm>

int main() {
    int new_num;
    std::cin >> new_num;
    int max = new_num, min = new_num;

    while (new_num) {
        max = std::max(max, new_num);
        min = std::min(min, new_num);
        std::cin >> new_num;
    }

    printf("%d %d\n", min, max);

    return 0;
}